Code of the Week #1: div(phi,U)
我们现在讨论一下这一行程序
fvm::div(phi, U);
这个经常出现在动量方程，表示左边第二项 $$ \frac{\partial U}{\partial t} + \nabla\cdot(UU) = -\nabla p + \nabla\cdot\tau $$
为了求解这个方程，需要经过一些推导，并对 $p$ 和 $U$ 进行解耦。但是，今天我们暂时不要讨论如何对解耦 $p$ 和 $U$。只讨论一下如何把 $\nabla\cdot(UU)$ 变成可进行计算的一小段程序。
实际上，动量方程是一个非线性的方程，但是直接求解这样一个非线性的方程，是很困难的。
因此，我们考虑将其中一个 $U$ 当成已知的 $U^* $，则 $$ \nabla\cdot(UU) = \nabla\cdot(U^* U) $$
而使用有限体积法时，需要对方程进行积分，这一项也不例外，这里考虑空间积分， $$ \iiint_\Omega\nabla \cdot(U^* U)\,dV =\iint_{\partial \Omega}(U^* U)\,d S= \sum(U^* U)\,dS＝\sum \vec{F}\cdot U $$ $d S$ 是离散单元的面，是有方向的。$\vec{F}$ 就是通量，通过这一网格时的总量。
获得这一公式后，需要完成某一网格上的格式，此格式就是对流格式。
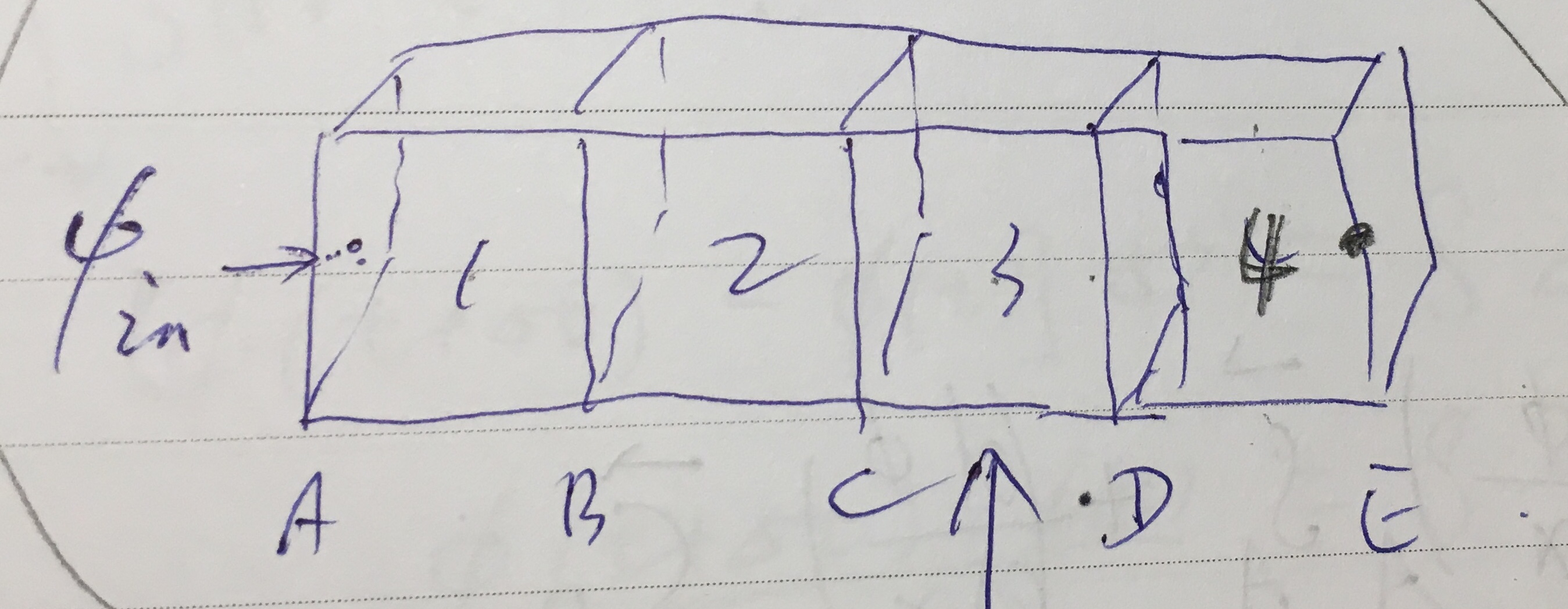
比如，考虑这样一个一维情况，有四个均分网格，编号 1 -- 4，其左右的面从左到右依次为 A -- E，在第 3 个网格上：
$$
(\sum\vec{F}\varphi)_3=\vec{F}_D\varphi_D + \vec{F}_C\varphi_C
$$
div(phi,U) 就是实现上面这个公式。
但是，要真正地实现可计算，还有几步要完成。首先，待求的值一般是指体心的值，而 $\varphi_C$ 是指面 C 上的值，而我们并不知道，因此，就需要插值，如果考虑以该面的相邻两个网格的线性平均值为该面上的值，这一插值方法称为中心差分，则 $$ \varphi_C=(\varphi_2+\varphi_3)/2\ \varphi_D=(\varphi_3+\varphi_4)/2 $$
当 $U^*$ 在整个空间都是相同的时候，针对面3时，$-\vec{F}_C=\vec{F}_D$，在求通量时，面的方向：向外为正，向内为负，因此，有 $$ (\sum\vec{F}\varphi)_3=\vec{F}_D(\varphi_D -\varphi_C)=\vec{F}_D\left(\frac{\varphi_2+\varphi_3}{2}-\frac{\varphi_3+\varphi_4}{2}\right)\ =\vec{F}_D\left(\frac{\varphi_2+\varphi_4}{2} \right) $$
不知道大家留意到没，我们需要求的变量 $\varphi_3$ 不见了。
对于边界 A，设已知 $\phi_A$，对于网格 1，有 $\phi_A - \dfrac{\varphi_1+\varphi_2}{2}$。
对于边界 D，设 $\varphi_D=\varphi_4$，对于网格 4，有 $-\dfrac{\varphi_3+\varphi_4}{2}+\varphi_4$
这四个网格，可组成一个矩阵乘法， $$ \left[ \begin{array}% 1 & 1 & 0 & 0\\ 1 & 0 &-1 & 0 \\ 0 & 1 & 0 & -1\\ 0 & 0 & -0.5 & 0.5 \end{array} \right] \times \left[ \begin{array}% \varphi_1\\ \varphi_2\\ \varphi_3\\ \varphi_4\\ \end{array} \right] $$
这一项再和动量方程的其他项相加，就可以完成该方程的离散化，可用矩阵计算的方法获得 $\varphi_i$ 的数值解。
对于获得面上的值的插值方法，在 OpenFOAM 中，其指定的方式是在 ./system/fvSchemes 里面的，如
divSchemes
{
div(phi,U) Gauss linear;
}
其中, Gauss 指的就是 $\sum$ 的方法，linear 就是插值的方法，但是，值得注意的地方就是对流项最少使用中心差分，主要原因是易形成矩阵主元除边界上的外，其他都为 0，这会造成矩阵求解困难。
在 OpenFOAM 的程序中，div 前面还有 fvm::，:: 意思是在某一名称空间下操作，fvm 表明该项表达式返回的值是矩阵系数。
如写成另外一种形式 fvc::div(phi,U) 则表明返回的是 $\nabla(UU)$ 的值。